Taking A Bayesian Approach to the 2025 Free Agent Class: Is Juan Soto Really the Crown Jewel?

This morning I stumbled on an article from Saul Forman on Fangraphs projecting risk in MLB using Bayesian techniques. I thought there was no better way to procrastinate my work for the day than to try my amateur hand at the same for the 2025 free agent class.

Why use Bayesian statistics at all? Traditionally, sabermetricians have used techniques such as delta-averaging and k-nearest neighbors to produce point estimates for player performance in future years. While useful in certain contexts, these methods are not optimal when predicting the performance of any given player. In the case of delta-averaging, the aging pattern for the average player does not necessarily translate well for outliers, such as Shohei Ohtani, who do not fit the mold of an average player. This is especially worrisome for teams since these players often comprise the vast majority of their financial investments. The k-nearest neighbors approach, which incorporates aging patterns of players that are "close" to a given player, is complicated by the issue of quantifying "closeness" between players across seasons and eras. Importantly, neither of these methods can quantify the uncertainty of a player’s future performance and only provide a point estimate rather than a probability distribution.

I decided to project players’ WAR over time to construct probability distributions for player performance rather than the point estimate predictions that are commonly used. Understanding these probability distributions can be immensely valuable to front offices when making free agency and trade decisions.

Suppose, for instance, that the GM for the Yankees receives a call from the Twins in February 2022 offering to trade Josh Donaldson, with two years left on his contract, in exchange for a stable of prospects. While the consensus is that the prospects will likely help the team in the long run, a 3.0 WAR 2022 season from Donaldson could elevate the Yankees from a projected wildcard team to legitimate World Series contenders. In this scenario, the probability distribution of future performance could serve as a crucial tool for the Yankees’ front office. If, for example, Donaldson is projected to have at least a 3.0 WAR in 70% of scenarios, that would make the trade far more enticing than if the probability were merely 20%.

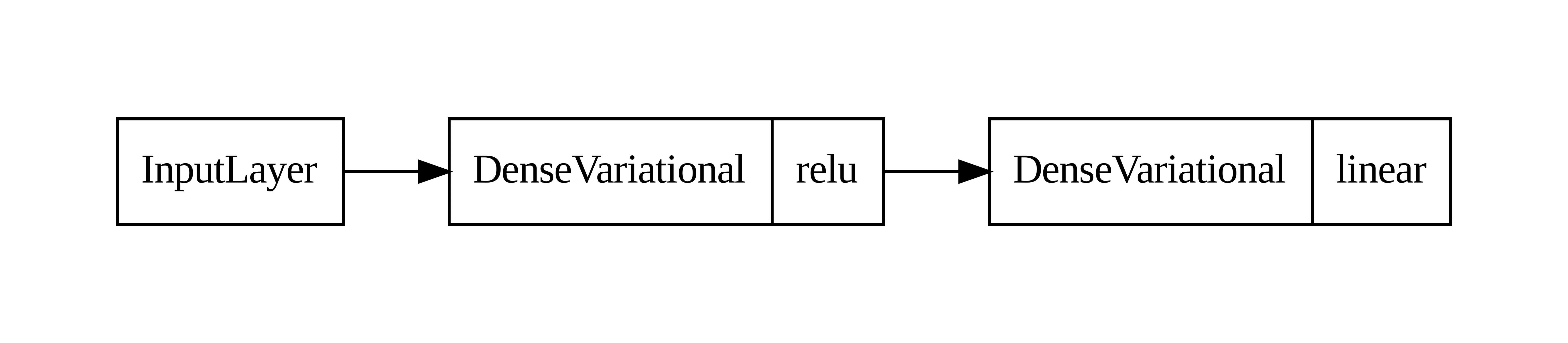
I began by constructing a Bayesian Neural Network (BNN), where weights are treated as probability distributions rather than fixed values to model this uncertainty. I predicted position player WAR in the upcoming season using available player seasons from Fangraphs spanning 2010-2024 with at least 100 PAs. The primary features used in the model include primary statistics such as WAR values over the previous three years and player age, as well as secondary statistics, including lags of plate appearances (PAs), weighted runs created plus (wRC+), walk percentage (BB%), strikeout percentage (K%), and adjusted batting average on balls in play (BABIP+). I also included lags of batting, fielding, base running, and positional value as features in the model. All features were standardized for model stability and performance and missing values were imputed with KNN (k = 5) and an 80-10-10 split for training, validation, and testing.

After testing models with one and two hidden layers and between 16 and 128 nodes in each layer (in increments of 16), I found that using one hidden layer with 16 nodes performed best on the validation set

Here is a sample prediction for Mookie Betts in 2024 (who was part of the test set):

I next created probability distributions for the top 10 position player free agents by projected WAR in 2025 and calculated the Sharpe ratio for each player. For those unfamiliar with the concept, the Sharpe ratio is often used in finance to calculate the risk-adjusted performance of an investment. It is calculated as follows where R^a is the return on asset a, R^b is the return on a risk-free asset (think treasury bonds), and σ is the standard deviation of returns (how volatile it is). The Sharpe ratio is high when expected excess returns are high and volatility is low, which is a desirable property for an investment.

In my analysis, I use WAR as a proxy for returns and use the calculated league average of 1.3 WAR as the risk-free rate of return similar to Forman. Here is the full output after our Sharpe calculations.

Unsurprisingly, Juan Soto has the largest Sharpe ratio, but what is more interesting is how closely Willy Adames tails him. While I would never consider Willy Adames to be in the same stratosphere as Soto, what's fascinating is that our model views him as almost as desirable of an investment as Soto when viewed through the lens of traditional frameworks used in finance.

Finally, I want to highlight how these probability distributions can be used to evaluate two much more similar players Ha-Seong Kim and Anthony Santander. Ha-Seong Kim has a higher expected WAR next year and a narrower spread (with a nearly 70% chance of having a higher WAR), making him a more enticing free agent target in a vacuum. While there are many other factors to consider beyond just their projected performance next year, I thought it was fun to waste a couple of hours on this and wanted to share it with you guys